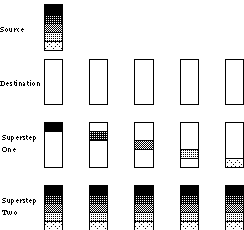
Figure 2: Two stage broadcast using total exchange.
Consider the problem of communicating a data-structure of size n (where n >= p) held on one process, into the memories of all p processors. A naive algorithm can be effected in a single superstep by having the broadcasting process perform p-1 distinct bsp_puts into the memories of each other process. As the broadcasting process transmits p-1 messages each of size n, the superstep realises an n(p-1)-relation with approximate cost (assuming p instead of p-1 in the above formulae):
| cost of one stage broadcast = npg + l | (5) |
where l is the up-front cost of performing a single superstep.

Figure 2: Two stage broadcast using total exchange.
It is clearly seen from the cost-formula captured in equation 5, that this algorithm is not scalable as its cost linearly increases with p. An alternative scalable BSP broadcasting algorithm, with cost 2g(n - (n/p)) + 2l is shown in Figure 2. The algorithm consists of two supersteps, that initially evenly distribute the data amongst the processes and subsequently perform a balanced communication involving all the processes. The cost of the distribution phase is (n/p)(p - 1)g + l as a single message of size (n/p) is sent to each of p - 1 processes. In the second superstep, every process sends and receives p-1 messages of size (n/p) from every other process. Surprisingly, the cost of this superstep is also (n/p)(p - 1)g + l; note that BSP cost analysis encourages balanced communication. The approximate cost (assuming p instead of p-1 in the above formulae) of the entire algorithm is determined by summing the cost of the two supersteps:
| cost of two stage broadcast = ((n/p)pg + l) + ((n/p)pg + l) = 2ng + 2l | (6) |
From equations 5 and 6 it is possible to determine the size of data for which the two-stage algorithm is superior to the one-stage algorithm:
For example, when l is large, and n and p are small, the cost of the extra superstep out-weighs the cost of communicating a few small messages. On the other hand, for large n or p, the communication cost out-weighs the overhead of the extra superstep.